Great-Circle
Great-Circle (대원)은 구의 중심을 지나는 평면이 구면과 만나서 생기는 원으로, 구면 위에서 그을 수 있는 가장 큰 원입니다. 지구에서는 적도와 모든 경선(자오선)이 대원에 해당합니다.
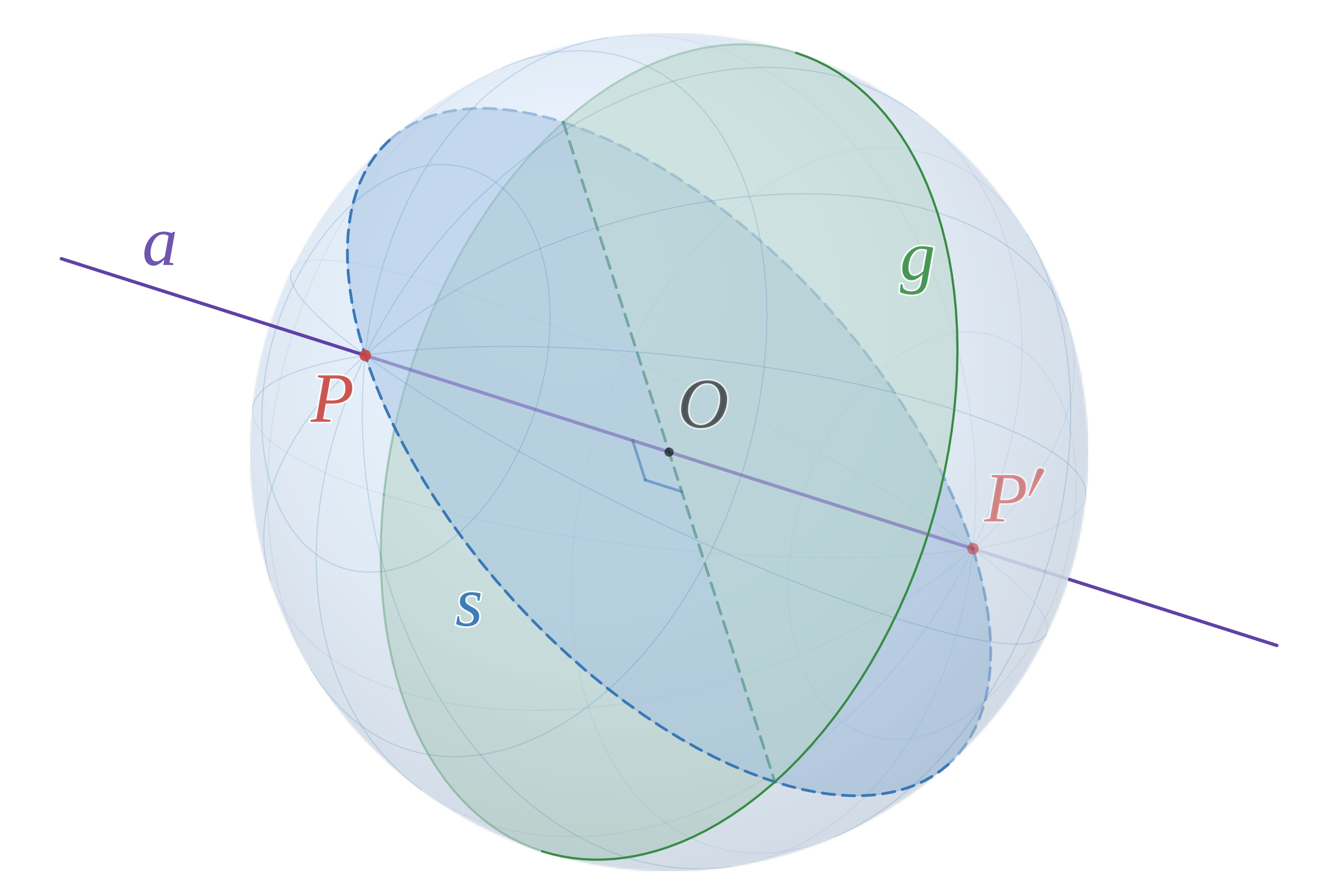
Great-Circle Distance
지구는 구형으로 평면 지도에서 보는 직선이 실제로는 최단 거리가 아닙니다. Great-circle distance는 구면(지구) 위의 두 점을 연결하는 최단 거리로 지구를 완전한 구로 가정했을 때, 두 지점을 잇는 가장 짧은 경로의 길이를 의미합니다.
Great-Circle Distance 계산 방법
Haversine Formula (하버사인 공식)
하버사인 공식은 구면 위의 두 점의 경도와 위도를 고려하여 대원 거리를 구합니다. 짧은 거리 계산에서 수치 안정성이 우수합니다. GPS, 모바일 앱, 포털 지도 등에서 일반적으로 사용됩니다. 거리 측정에서 가장 많이 사용되는 방식입니다.
$$d = \sin^2\left(\frac{\Delta\varphi}{2}\right) + \cos\varphi_1 \cdot \cos\varphi_2 \cdot \sin^2\left(\frac{\Delta\lambda}{2}\right)$$
d = 2r × arcsin(√(sin²(Δφ/2) + cos(φ1) × cos(φ2) × sin²(Δλ/2)))
- d: great-circle distance
- r: 지구 반지름 (약 6,371km)
- φ1, φ2: 두 지점의 위도 (라디안)
- Δφ: 위도 차이 - Δλ: 경도 차이
import org.locationtech.jts.geom.Coordinate;
public class HaversineCalculator {
// 지구 평균 반지름 (미터)
private static final double EARTH_RADIUS_METERS = 6371000.0;
/**
* 하버사인 공식으로 계산
* @param coord1 시작 좌표 (경도, 위도)
* @param coord2 도착 좌표 (경도, 위도)
* @return 거리 (미터)
*/
public static double calculateHaversine(Coordinate coord1, Coordinate coord2) {
double lat1 = Math.toRadians(coord1.getY());
double lon1 = Math.toRadians(coord1.getX());
double lat2 = Math.toRadians(coord2.getY());
double lon2 = Math.toRadians(coord2.getX());
double deltaLat = lat2 - lat1;
double deltaLon = lon2 - lon1;
double a = Math.sin(deltaLat/2) * Math.sin(deltaLat/2) +
Math.cos(lat1) * Math.cos(lat2) *
Math.sin(deltaLon/2) * Math.sin(deltaLon/2);
double c = 2 * Math.atan2(Math.sqrt(a), Math.sqrt(1-a));
return EARTH_RADIUS * c;
}
}
Spherical Law of Cosines (구면 코사인 법칙)
구면 코사인 법칙은 두 지점이 매우 가까울수록 floating-point 오차가 커질 수 있다는 단점이 있습니다.
$$d = R \cdot \arccos\big(\sin\varphi_1 \cdot \sin\varphi_2 + \cos\varphi_1 \cdot \cos\varphi_2 \cdot \cos(\lambda_2 - \lambda_1)\big)$$
import org.locationtech.jts.geom.Coordinate;
public class SphericalLawOfCosines {
// 지구 평균 반지름 (미터)
private static final double EARTH_RADIUS_METERS = 6371000.0;
/**
* 구면 코사인 법칙을 사용한 거리 계산
* @param coord1 시작 좌표 (경도, 위도)
* @param coord2 도착 좌표 (경도, 위도)
* @return 거리 (미터)
*/
public static double calculateSphericalDistance(Coordinate coord1, Coordinate coord2) {
// 위도, 경도를 라디안으로 변환
double lat1 = Math.toRadians(coord1.getY());
double lon1 = Math.toRadians(coord1.getX());
double lat2 = Math.toRadians(coord2.getY());
double lon2 = Math.toRadians(coord2.getX());
// 경도 차이
double deltaLon = lon2 - lon1;
// 구면 코사인 법칙 공식
// cos(c) = cos(a) * cos(b) + sin(a) * sin(b) * cos(C)
// 여기서 a = 90° - lat1, b = 90° - lat2, C = deltaLon
double centralAngle = Math.acos(
Math.sin(lat1) * Math.sin(lat2) +
Math.cos(lat1) * Math.cos(lat2) * Math.cos(deltaLon)
);
// 호장 길이 = 반지름 × 중심각(라디안)
return EARTH_RADIUS_METERS * centralAngle;
}
}
Vincenty Formula (타원체 지구 모델)
위경도 기반으로 반복 계산(iterative method)를 통한 고정밀 결과를 반영할 수 있습니다. 대륙 간 거리, 측량 등에서 높은 정확도를 가집니다. 하지만 구현이 복잡하고 계산량이 많은 단점이 있습니다.
'Dev Stories > 지리정보(Spatial)' 카테고리의 다른 글
| LX 디지털트윈이 가져다 주는 스마트시티 (요약보고서) (0) | 2025.11.13 |
|---|---|
| [MapLibre] Projection 변환시 발생되는 렌더링 오류 (0) | 2025.09.08 |
| Vector Tile Server 벡터 타일 서버 (0) | 2025.06.12 |
| Vector Tiles 벡터 타일 (0) | 2025.06.12 |
| 공간 인덱스(Spatial Index)를 구성하는 작동할까? (0) | 2025.06.10 |



